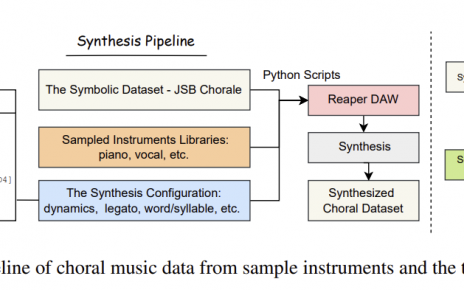
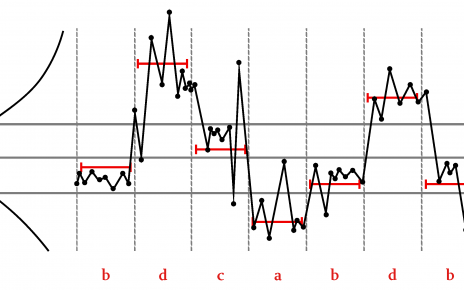
Gonzalo Romero-García. Mathematical Morphology for the Analysis and Generation of TimeFrequency Representations of Music. Signal and Image Processing. Sorbonne Université, 2023. English. ffNNT : 2023SORUS554ff. fftel-04470770f
Abstract: This thesis explores the application of Mathematical Morphology to the analysis and generation of music, focusing on two time-frequency representations: spectrograms and piano rolls. Mathematical Morphology is a nonlinear image processing tool that serves to consider topological notions of the image. We present three applications. The first is to analyze spectrograms with morphological tools to obtain parameters with which to synthesize a musical instrument sound. The second is to generate piano rolls with two musical parameters, texture and harmony, by arranging them through morphological dilation. The third is to apply morphological operators to analyze piano rolls using graph theory. The thesis thus proposes new approaches for problems in sound analysis and computational musicology.