Predictive Quantization and Symbolic Dynamics

 

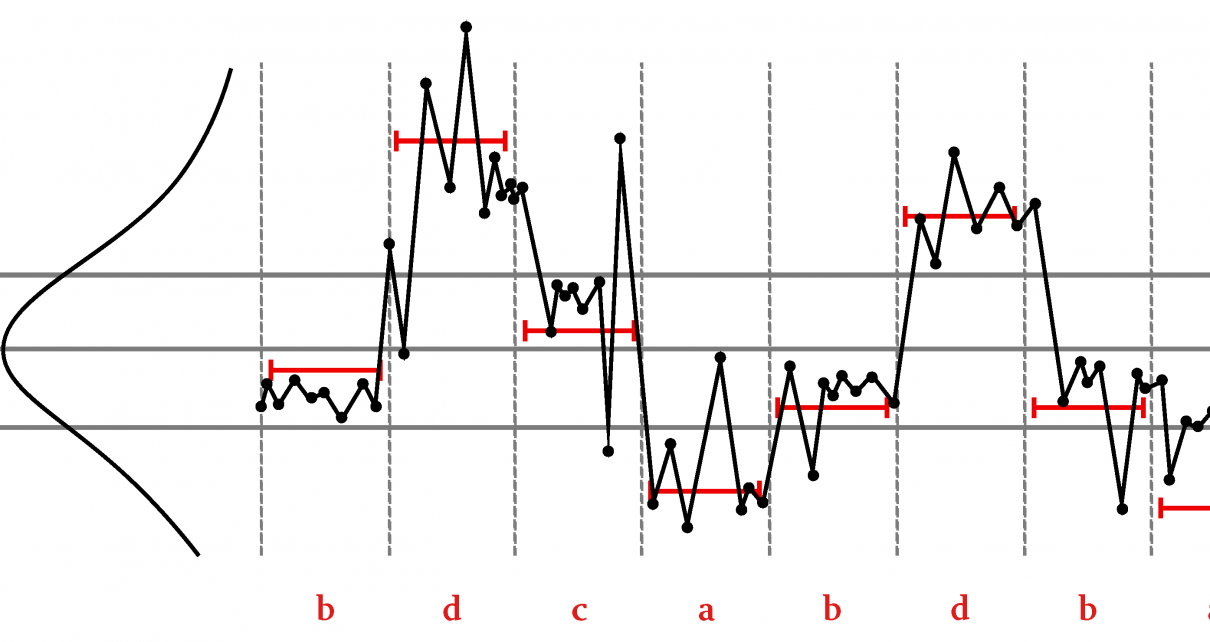
Abstract: Capturing long-term statistics of signals and time series is important for modeling recurrent phenomena, especially when such recurrences are a-periodic and can be characterized by the approximate repetition of variable length motifs, such as patterns in human gestures and trends in financial time series or musical melodies. Regressive and auto-regressive models that are common in such problems, both analytically derived and neural network-based, often suffer from limited memory or tend to accumulate errors, making them sensitive during training. Moreover, such models often assume stationary signal statistics, which makes it difficult to deal with switching regimes or conditional signal dynamics. In this paper, we describe a method for time series modeling that is based on adaptive symbolization that maximizes the predictive information of the resulting sequence. Using approximate string-matching methods, the initial vectorized sequence is quantized into a discrete representation with a variable quantization threshold. Finding an optimal signal embedding is formulated in terms of a predictive bottleneck problem that takes into account the trade-off between representation and prediction accuracy. Several downstream applications based on discrete representation are described in this paper, which includes an analysis of the symbolic dynamics of recurrence statistics, motif extraction, segmentation, query matching, and the estimation of transfer entropy between parallel signals.